Quickstart

Usage

You can use XSpline as a univariate function or use it to get design matrix.

import numpy as np
import matplotlib.pyplot as plt
from xspline import XSpline

spline = XSpline(knots=[0, 0.25, 0.5, 0.75, 1], degree=3)
x = np.arange(0, 1.01, 0.01)

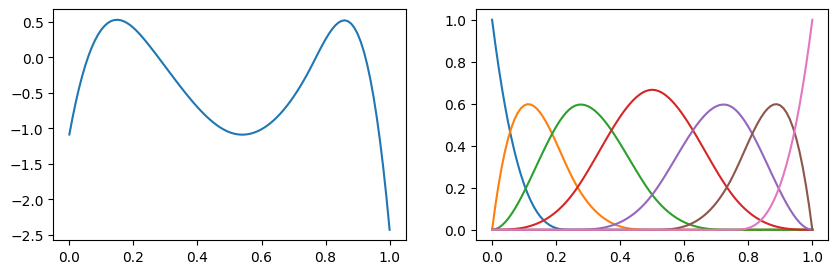
One is to use XSpline as a univariate function. In this case, user must provide coefficients for the spline bases.

np.random.seed(123)
spline.coef = np.random.randn(len(spline))
y, design_mat = spline(x), spline.get_design_mat(x)

fig, ax = plt.subplots(1, 2, figsize=(10, 3))
ax[0].plot(x, y)
ax[1].plot(x, design_mat)

XSpline can be used to obtain derivatives.

dy, ddesign_mat = spline(x, order=1), spline.get_design_mat(x, order=1)

fig, ax = plt.subplots(1, 2, figsize=(10, 3))
ax[0].plot(x, dy)
ax[1].plot(x, ddesign_mat)

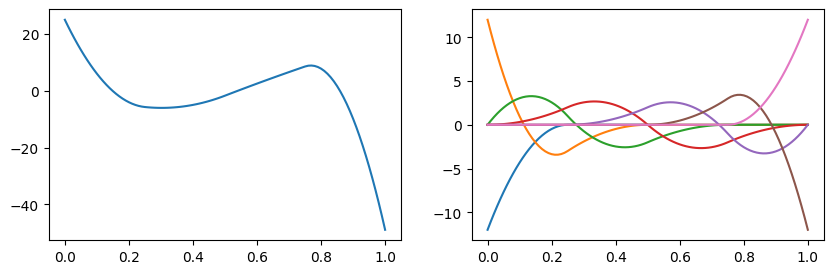
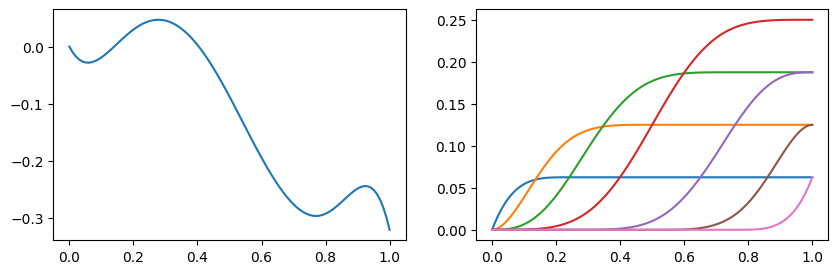
XSpline can be used to obtain definite integrals.

iy, idesign_mat = spline(x, order=-1), spline.get_design_mat(x, order=-1)

fig, ax = plt.subplots(1, 2, figsize=(10, 3))
ax[0].plot(x, iy)
ax[1].plot(x, idesign_mat)

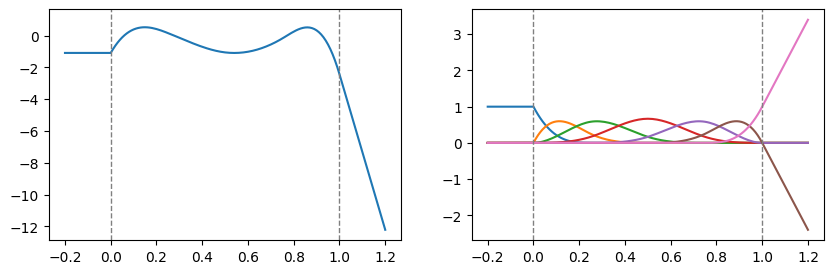
XSpline can extrapolate with different polynomial options

np.random.seed(123)
# constant extrapolation one the left and linear extrapolation on the right
spline = XSpline(
    knots=[0, 0.25, 0.5, 0.75, 1],
    degree=3,
    ldegree=0,
    rdegree=1,
    coef=np.random.randn(len(spline)),
)
x = np.arange(-0.5, 1.51, 0.01)
y, design_mat = spline(x), spline.get_design_mat(x)

fig, ax = plt.subplots(1, 2, figsize=(10, 3))
ax[0].plot(x, y)
ax[1].plot(x, design_mat)
for i in range(len(ax)):
    ax[i].vlines(
        [0, 1],
        ymin=0,
        ymax=1,
        transform=ax[i].get_xaxis_transform(),
        linestyle="--",
        linewidth=1,
        color="grey",
    )